Anthropics
Abstract:
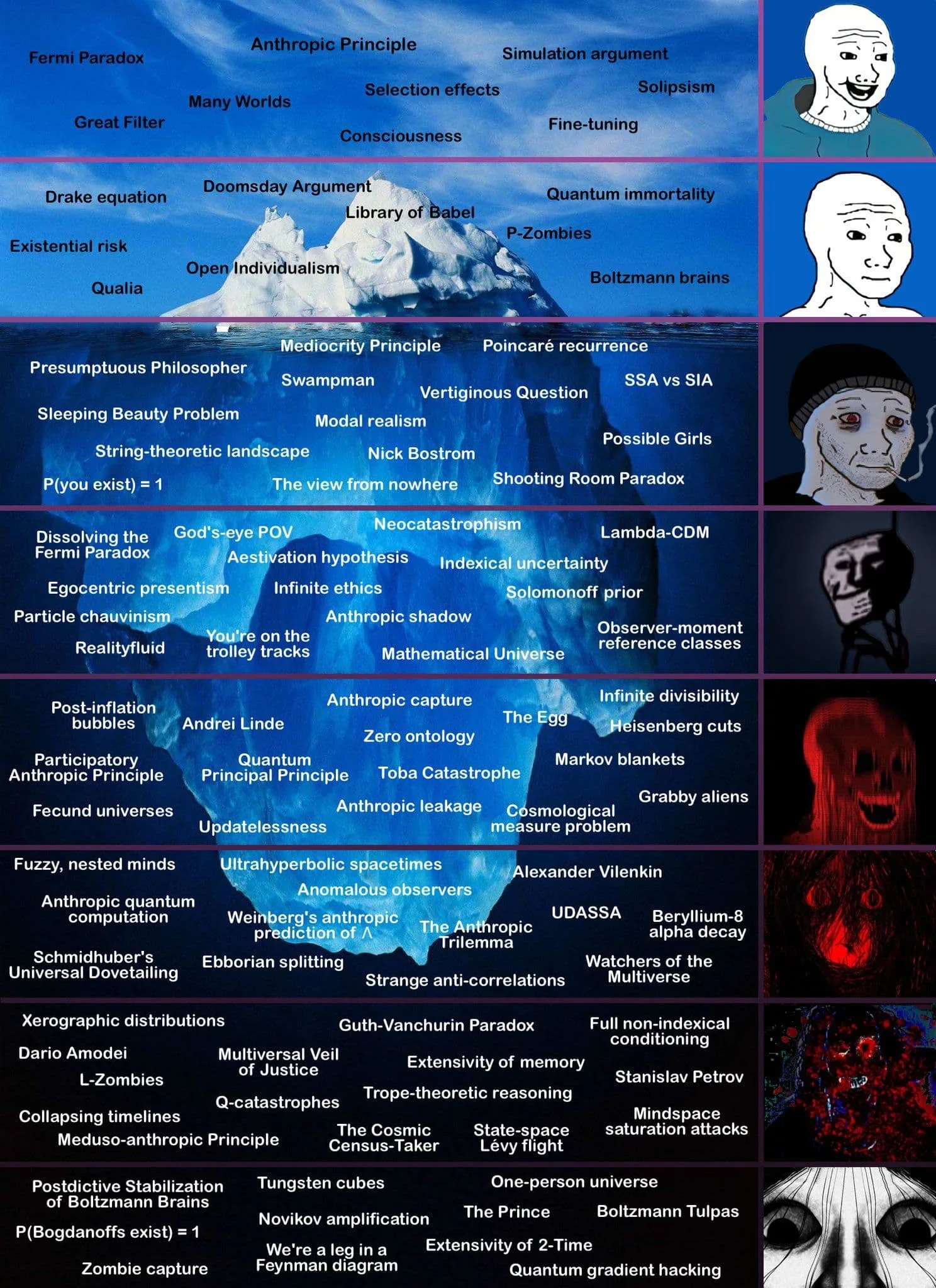
This project surveys the role of anthropic reasoning in decision theory, probability, and AI alignment. It will compile and systematize frameworks such as the Self-Sampling Assumption (SSA), Self-Indication Assumption (SIA), anthropic capture, the Doomsday argument, anthropic decision theory (ADT), and infra-Bayesian approaches. The project will also analyze how anthropic reasoning interacts with multi-agent settings, simulation arguments, and AI alignment scenarios involving observer-selection effects. The aim is to distill a clear taxonomy of anthropic principles, their paradoxes, and their implications for reasoning under uncertainty when agents must account for their own indexical information. Part of the project will be to run an Anthropics Conference.
This project surveys the role of anthropic reasoning in decision theory, probability, and AI alignment. It will compile and systematize frameworks such as the Self-Sampling Assumption (SSA), Self-Indication Assumption (SIA), anthropic capture, the Doomsday argument, anthropic decision theory (ADT), and infra-Bayesian approaches. The project will also analyze how anthropic reasoning interacts with multi-agent settings, simulation arguments, and AI alignment scenarios involving observer-selection effects. The aim is to distill a clear taxonomy of anthropic principles, their paradoxes, and their implications for reasoning under uncertainty when agents must account for their own indexical information. Part of the project will be to run an Anthropics Conference.
Keywords: anthropics, SSA, SIA, anthropic decision theory, doomsday argument, anthropic capture, observer selection, simulation argument, indexical information, infra-Bayesian physicalism
People: TBD